CLV Quickstart

Note

This quickstart was adapted from the legacy lifetimes library. Some pictures and descriptions are directly attributable to the lifetimes developers.

In this notebook we will be using the CDNOW dataset, a popular benchmarking dataset in CLV and Buy Till You Die (BTYD) modeling research. Data is available here, with additional details [here].

import arviz as az
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from arviz.labels import MapLabeller

from pymc_marketing import clv

az.style.use("arviz-darkgrid")

%config InlineBackend.figure_format = "retina" # nice looking plots

1.1 Data Requirements

For all models, the following nomenclature is used:

• customer_id represents a unique identifier for each customer.

• frequency represents the number of repeat purchases that a customer has made, i.e. one less than the total number of purchases.

• T represents a customer’s “age”, i.e. the duration between a customer’s first purchase and the end of the period of study. In this example notebook, the units of time are in weeks.

• recency represents the timepoint when a customer made their most recent purchase. This is also equal to the duration between a customer’s first non-repeat purchase (usually time 0) and last purchase. If a customer has made only 1 purchase, their recency is 0;

• monetary_value represents the average value of a given customer’s repeat purchases. Customers who have only made a single purchase have monetary values of zero.

If working with raw transaction data, the rfm_summary function can be used to preprocess data for modeling:

raw_trans = pd.read_csv("https://raw.githubusercontent.com/pymc-labs/pymc-marketing/main/data/cdnow_transactions.csv")

raw_trans.head(5)

	_id	id	date	cds_bought	spent
0	4	1	19970101	2	29.33
1	4	1	19970118	2	29.73
2	4	1	19970802	1	14.96
3	4	1	19971212	2	26.48
4	21	2	19970101	3	63.34

rfm_data = clv.utils.rfm_summary(
    raw_trans,
    customer_id_col = "id",
    datetime_col = "date",
    monetary_value_col = "spent",
    datetime_format = "%Y%m%d",
    time_unit = "W")

rfm_data

	customer_id	frequency	recency	T	monetary_value
0	1	3.0	49.0	78.0	23.723333
1	2	1.0	2.0	78.0	11.770000
2	3	0.0	0.0	78.0	0.000000
3	4	0.0	0.0	78.0	0.000000
4	5	0.0	0.0	78.0	0.000000
...	...	...	...	...	...
2352	2353	2.0	53.0	66.0	19.775000
2353	2354	5.0	24.0	66.0	44.928000
2354	2355	1.0	44.0	66.0	24.600000
2355	2356	6.0	62.0	66.0	31.871667
2356	2357	0.0	0.0	66.0	0.000000

2357 rows × 5 columns

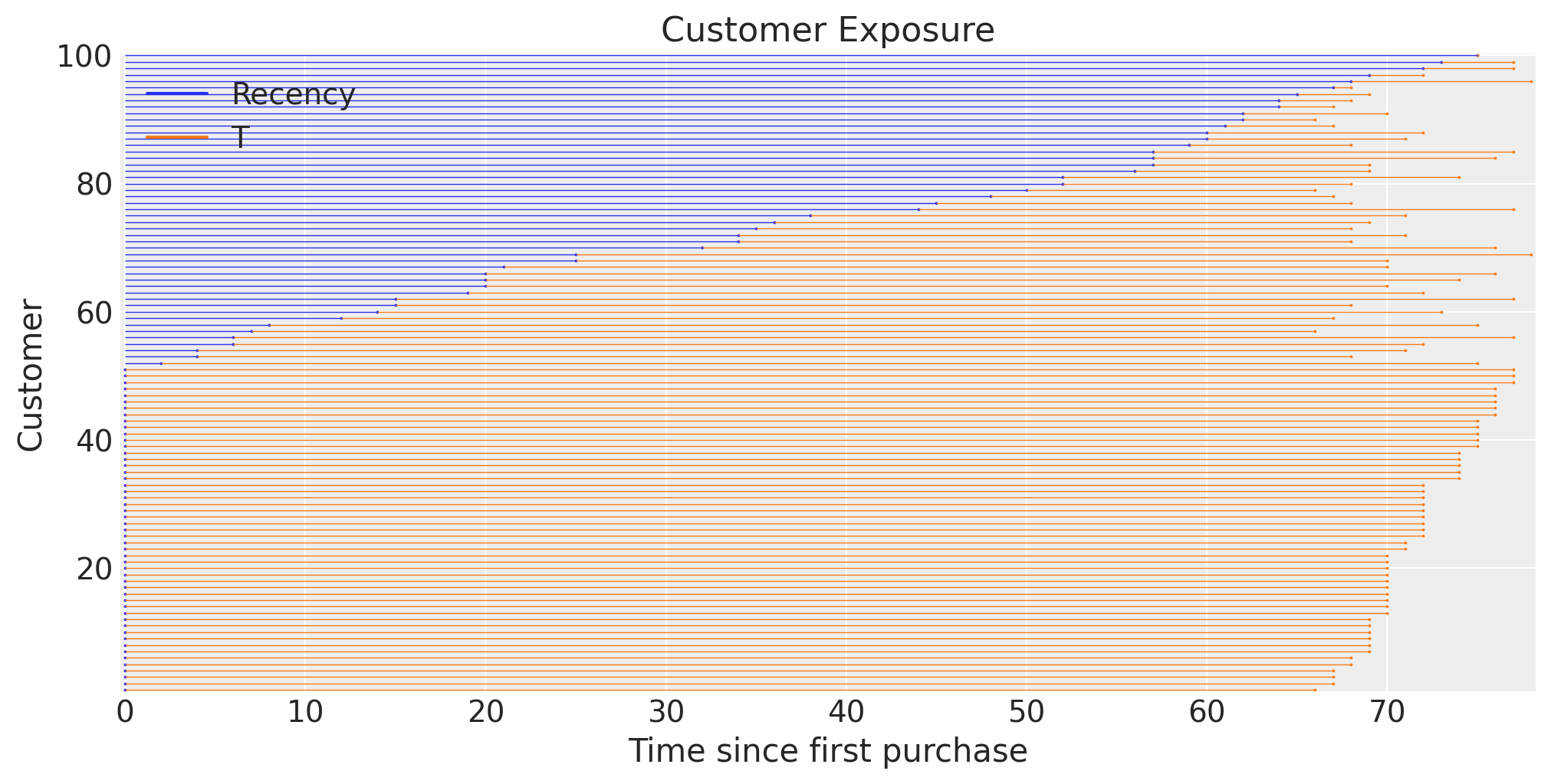
To visualize data in RFM format, we can plot the recency and T of the customers with the plot_customer_exposure function. We see a large chunk (>60%) of customers haven’t made another purchase in a while.

fig, ax = plt.subplots(figsize=(10, 5))
(
    rfm_data
    .sample(n=100, random_state=42)
    .sort_values(["recency", "T"])
    .pipe(clv.plot_customer_exposure, ax=ax, linewidth=0.5, size=0.75)
);

Basic Frequency/Recency analysis using the BG/NBD model

As this dataset represents non-contractual transactions in the continuous time domain, we will use the Beta-Geometric/Negative Binomial Distribution (BG/NBD) model to infer the frequency of repeat purchases for each customer in the dataset. The Pareto/Negative Binomial Distribution (Pareto/NBD) model is also available as an alternative if you wish to compare results.

For use cases involving discrete time, contractual transactions, use the Shifted Beta-Geometric model.

bgm = clv.BetaGeoModel(
    data = rfm_data
)
bgm.build_model()

This model has 4 parameters that specify the global frequency and dropout rates of customers.

bgm

BG/NBD
         a ~ HalfFlat()
         b ~ HalfFlat()
     alpha ~ HalfFlat()
         r ~ HalfFlat()
likelihood ~ Potential(f(r, alpha, b, a))

The default priors for the 4 parameters follow a HalfFlat distribution, which is an improper positive uniform distribution. For small datasets this prior can yield implausible posteriors. To avoid this problem, more informative priors can be specified by defining custom PyMC distributions.

Here, we will replace the HalfFlat default by more well-behaved HalfNormal priors with a standard deviation of 10. Customization priors is possible by passing a dictionary with keys being the name of the prior, and values being a dictionary with 2 keys: ‘dist’ representing the name of PyMC distribution and ‘kwargs’ that holds an optional dictionary of all parameters we wish to pass to the distribution

model_config = {
    'a_prior': {'dist': 'HalfNormal',
                'kwargs': {'sigma': 10}},
    'b_prior': {'dist': 'HalfNormal',
                'kwargs': {'sigma': 10}},
    'alpha_prior': {'dist': 'HalfNormal',
                'kwargs': {'sigma': 10}},
    'r_prior': {'dist': 'HalfNormal',
                'kwargs': {'sigma': 10}},
}

bgm = clv.BetaGeoModel(
    data = rfm_data,
    model_config = model_config,
)
bgm.build_model()
bgm

BG/NBD
         a ~ HalfNormal(0, 10)
         b ~ HalfNormal(0, 10)
     alpha ~ HalfNormal(0, 10)
         r ~ HalfNormal(0, 10)
likelihood ~ Potential(f(r, alpha, b, a))

Having specified the model, we can now fit it.

bgm.fit()
bgm.fit_summary()

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [a, b, alpha, r]

100.00% [8000/8000 00:07<00:00 Sampling 4 chains, 0 divergences]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 8 seconds.

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
a	0.695	0.163	0.409	0.975	0.004	0.003	1642.0	1782.0	1.0
b	3.312	1.016	1.652	5.116	0.026	0.019	1646.0	1700.0	1.0
alpha	7.093	0.513	6.129	8.066	0.013	0.009	1612.0	1745.0	1.0
r	0.276	0.012	0.255	0.300	0.000	0.000	1618.0	1689.0	1.0

We can use ArviZ, a Python library tailored to produce visualizations for Bayesian models, to plot the posterior distribution of each parameter.

az.plot_posterior(bgm.fit_result);

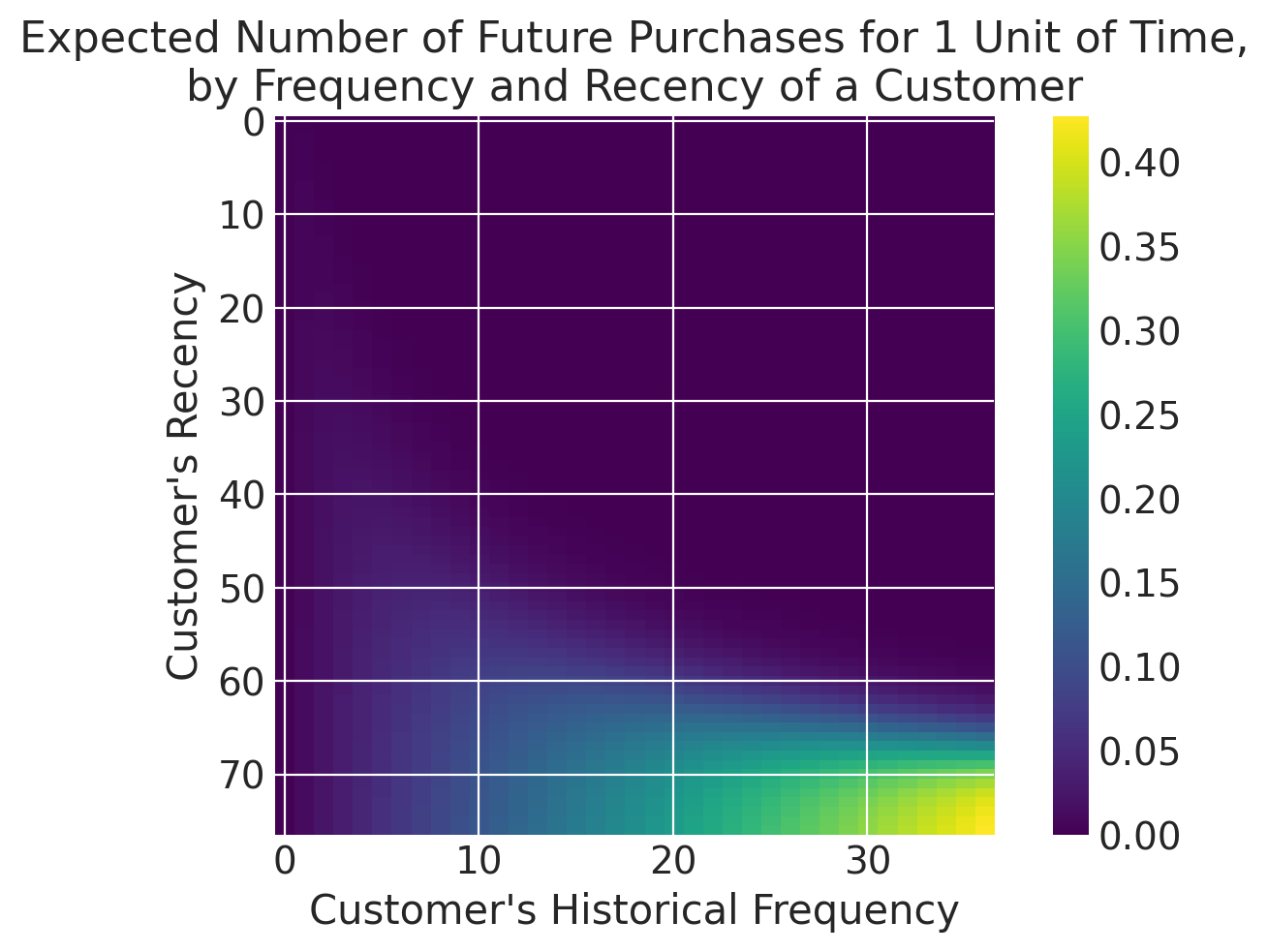
Visualizing the Frequency/Recency Matrix

clv.plot_frequency_recency_matrix(bgm);

We can see our best customers have been active for over 60 weeks and have made over 20 purchases (bottom-right). Note the “tail” sweeping up towards the upper-left corner - these customers are infrequent and/or may not have purchased recently. What is the probability they are still active?

clv.plot_probability_alive_matrix(bgm)

<Axes: title={'center': 'Probability Customer is Alive,\nby Frequency and Recency of a Customer'}, xlabel="Customer's Historical Frequency", ylabel="Customer's Recency">

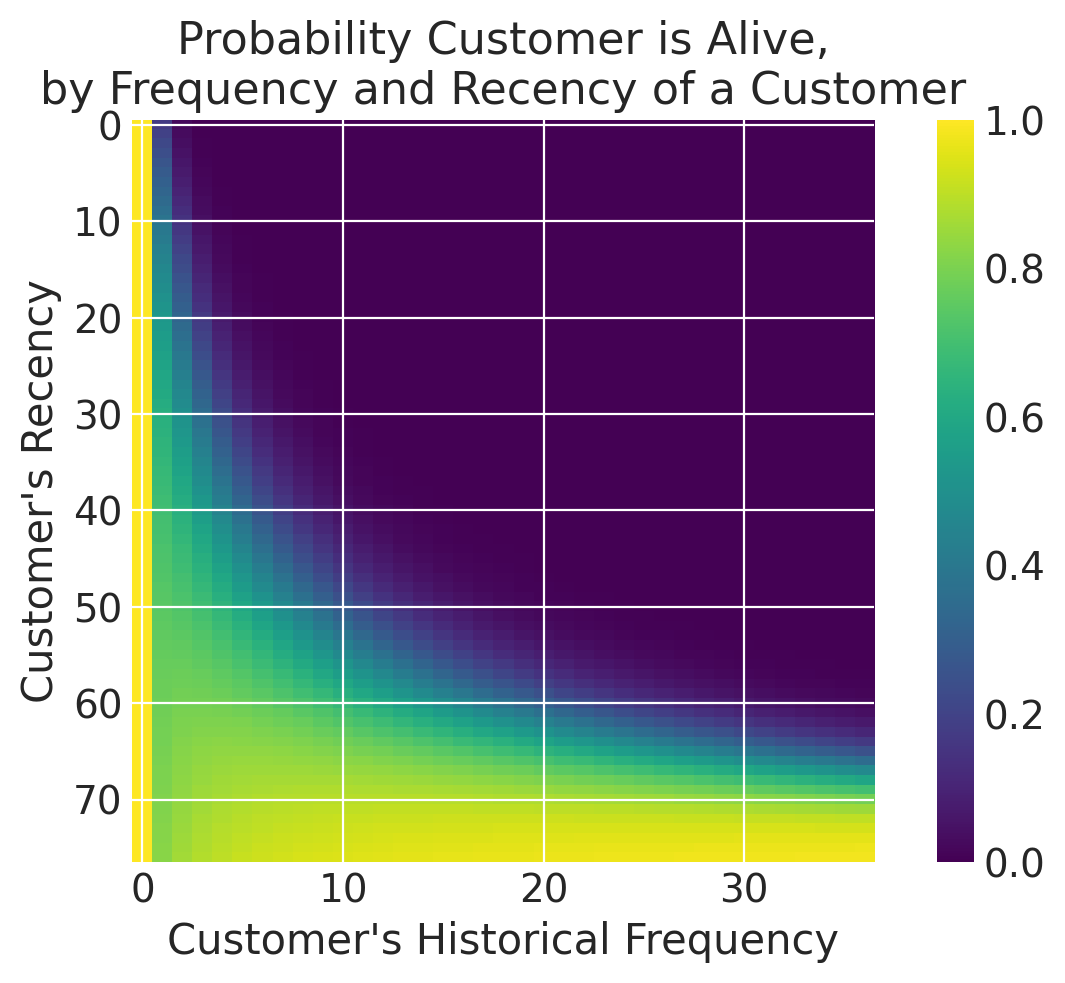
Note that all non-repeat customers have an alive probability of 1, which is one of the quirks of BetaGeoModel. In many use cases this is still a valid assumption, but if non-repeat customers are a key focus in your use case, you may want to try ParetoNBDModel instead.

Looking at the probability alive matrix, we can infer that customers who have made fewer purchases are less likely to return, and may be worth targeting for retention.

Ranking customers from best to worst

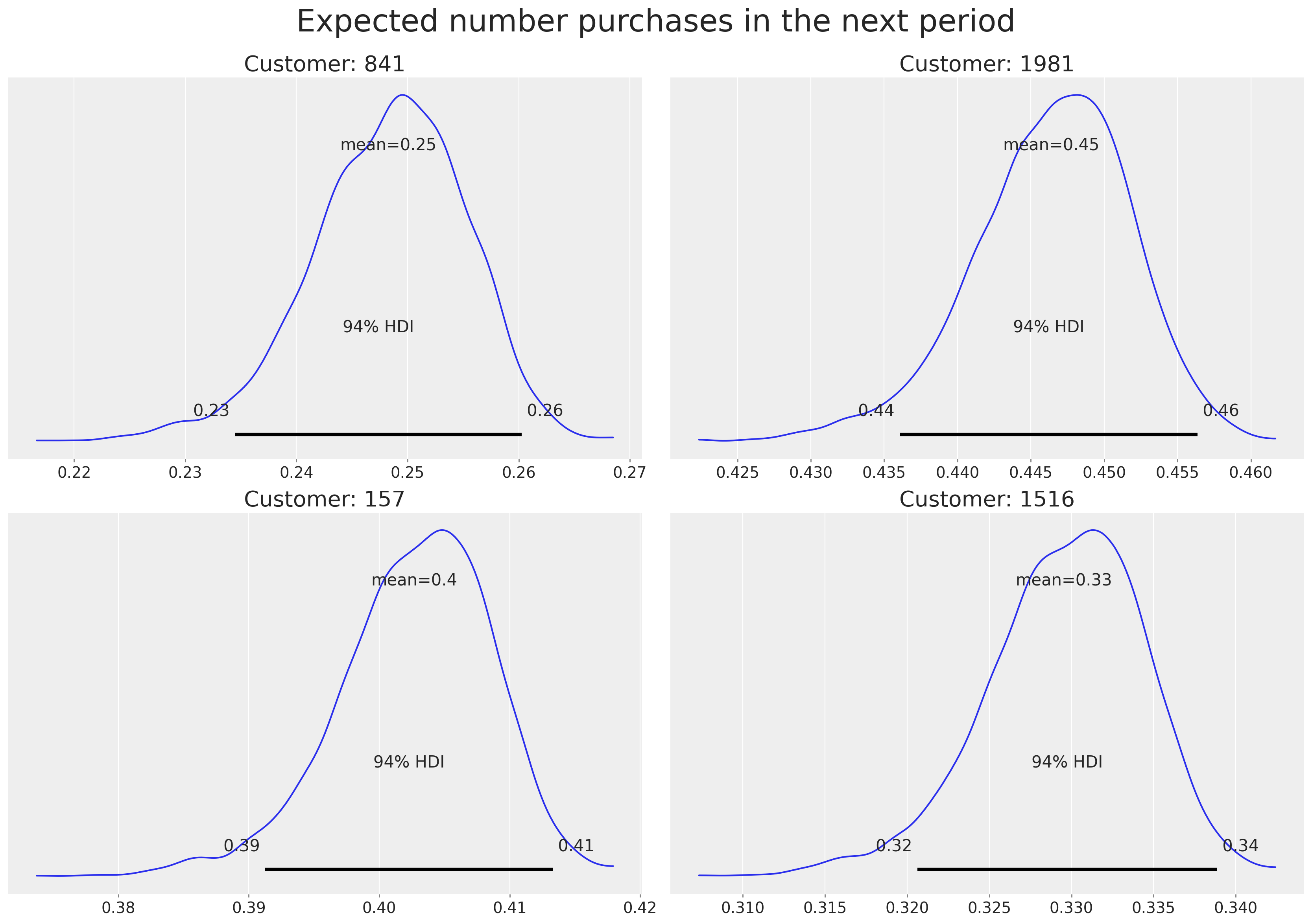
Having fit the model, we can ask what is the expected number of purchases for our customers in the next period. Let’s look at the four more promising customers.

num_purchases = bgm.expected_num_purchases(
    customer_id=rfm_data["customer_id"],
    t=1,
    frequency=rfm_data["frequency"],
    recency=rfm_data["recency"],
    T=rfm_data["T"]
)

sdata = rfm_data.copy()
sdata["expected_purchases"] = num_purchases.mean(("chain", "draw")).values
sdata.sort_values(by="expected_purchases").tail(4)

	customer_id	frequency	recency	T	monetary_value	expected_purchases
812	813	30.0	72.0	74.0	35.654000	0.355740
1202	1203	32.0	71.0	72.0	47.172187	0.394494
156	157	36.0	74.0	77.0	30.603611	0.402683
1980	1981	35.0	66.0	68.0	46.748857	0.446398

We can plot the uncertainty in the expected number of purchases in the next period.

ids = [841, 1981, 157, 1516]
ax = az.plot_posterior(num_purchases.sel(customer_id=ids), grid=(2, 2))
for axi, id in zip(ax.ravel(), ids, strict=False):
    axi.set_title(f"Customer: {id}", size=20)
plt.suptitle("Expected number purchases in the next period", fontsize=28, y=1.05);

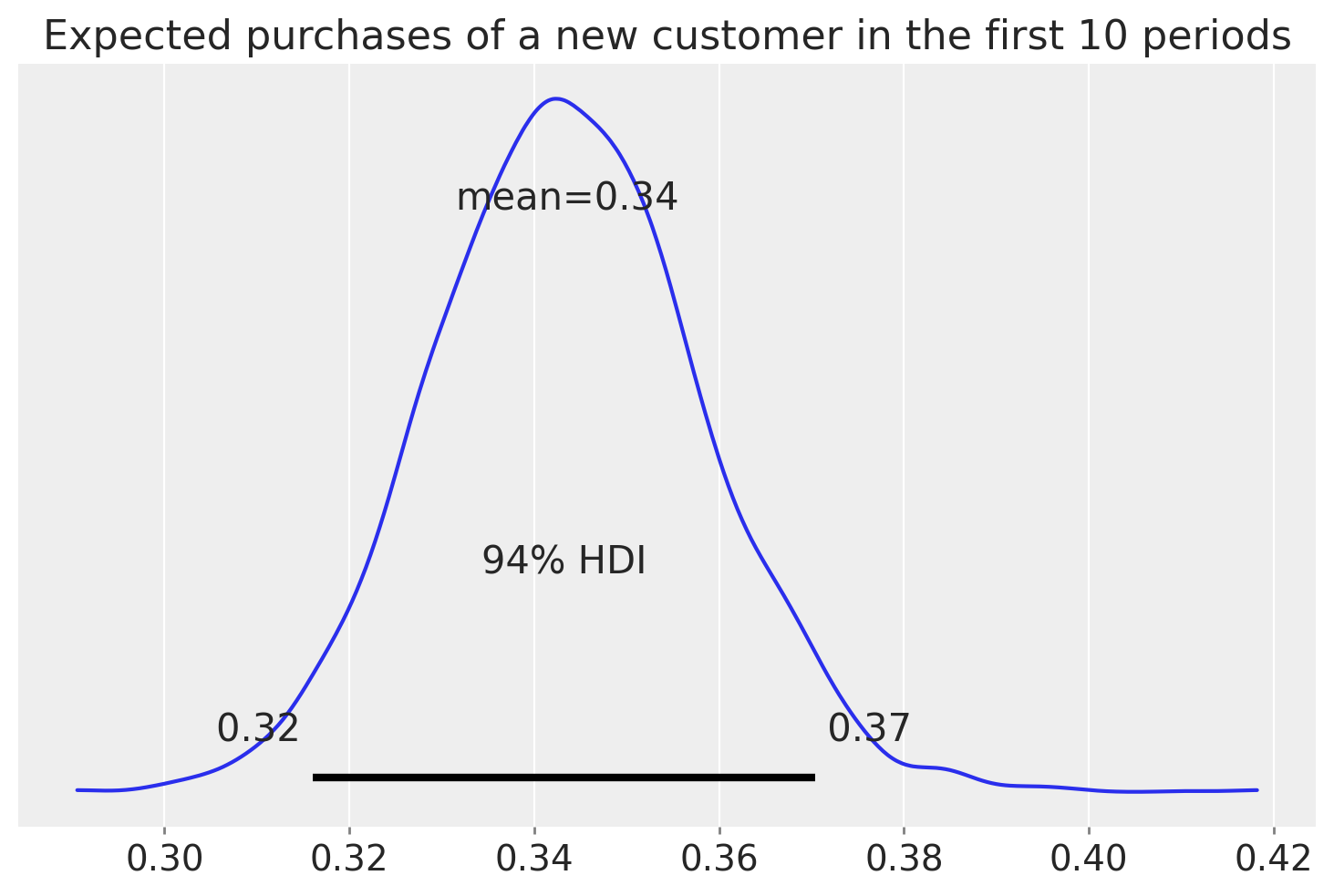
Predicting purchase behavior of a new customer

We can use the fitted model to predict the number of purchases for a fresh new customer.

az.plot_posterior(
    bgm.expected_num_purchases_new_customer(t=10)
)
plt.title("Expected purchases of a new customer in the first 10 periods");

Customer Probability Histories

Given a customer transaction history, we can calculate their historical probability of being alive, according to our trained model.

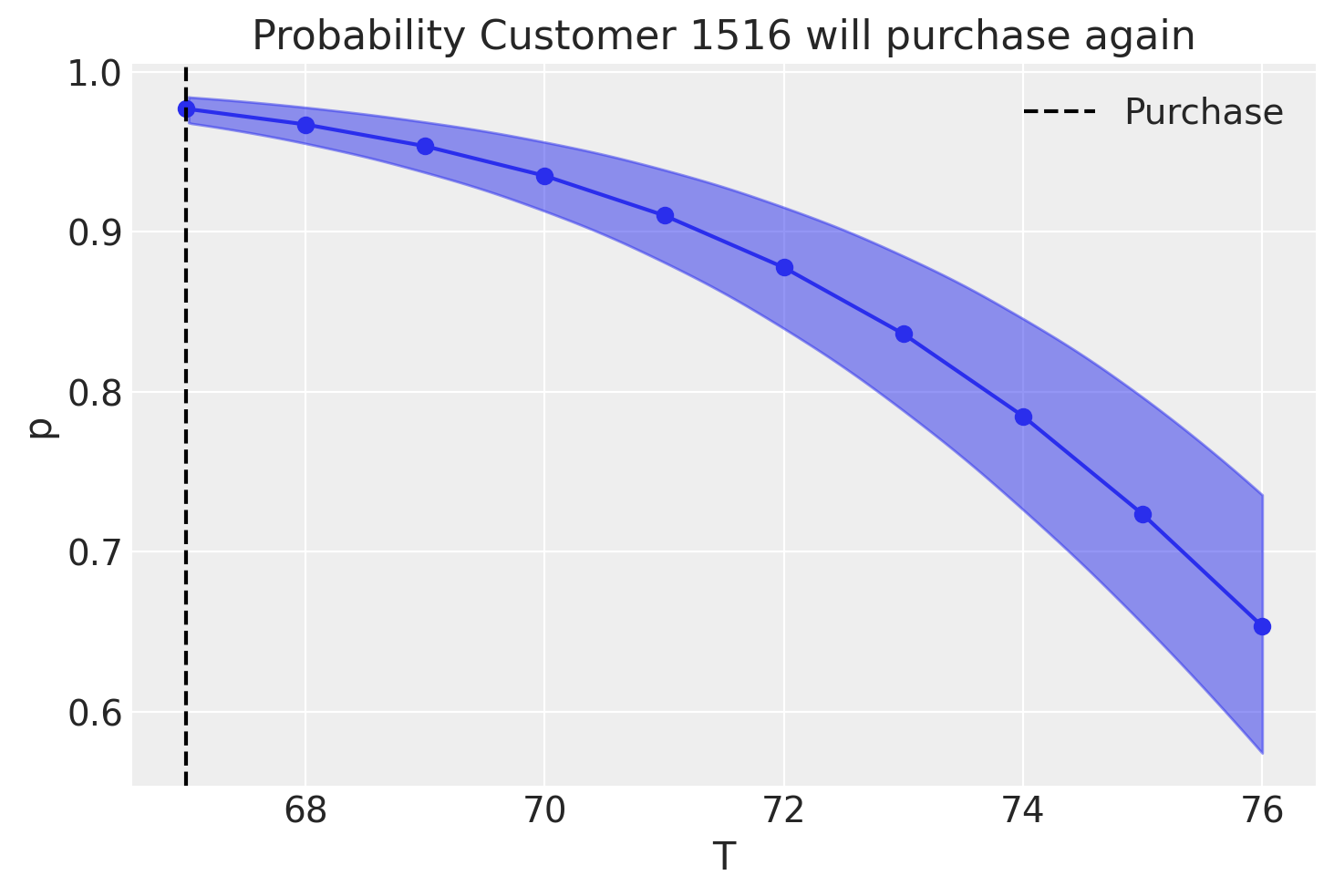
Let look at active customer 1516 and assess the change in probability that the user will ever return if they do no other purchases in the next 9 time periods.

customer_1516 = rfm_data.loc[1515]
customer_1516

customer_id       1516.000000
frequency           27.000000
recency             67.000000
T                   70.000000
monetary_value      51.944074
Name: 1515, dtype: float64

customer_1516_history = pd.DataFrame(dict(
    ID=np.full(10, 1515, dtype="int"),
    frequency=np.full(10, customer_1516["frequency"], dtype="int"),
    recency=np.full(10, customer_1516["recency"]),
    T=(np.arange(0, 10) + customer_1516["recency"]).astype("int"),

))
customer_1516_history

	ID	frequency	recency	T
0	1515	27	67.0	67
1	1515	27	67.0	68
2	1515	27	67.0	69
3	1515	27	67.0	70
4	1515	27	67.0	71
5	1515	27	67.0	72
6	1515	27	67.0	73
7	1515	27	67.0	74
8	1515	27	67.0	75
9	1515	27	67.0	76

p_alive = bgm.expected_probability_alive(
    customer_id=customer_1516_history["ID"],
    frequency=customer_1516_history["frequency"],
    recency=customer_1516_history["recency"],
    T=customer_1516_history["T"],
)

az.plot_hdi(customer_1516_history["T"], p_alive, color="C0")
plt.plot(customer_1516_history["T"], p_alive.mean(("draw", "chain")), marker="o")
plt.axvline(customer_1516_history["recency"].iloc[0], c="black", ls="--", label="Purchase")

plt.title("Probability Customer 1516 will purchase again")
plt.xlabel("T")
plt.ylabel("p")
plt.legend();

We can see that, if no purchases are being made in the next 9 weeks, the model has low confidence that the costumer will ever return. What if they had done one purchase in between?

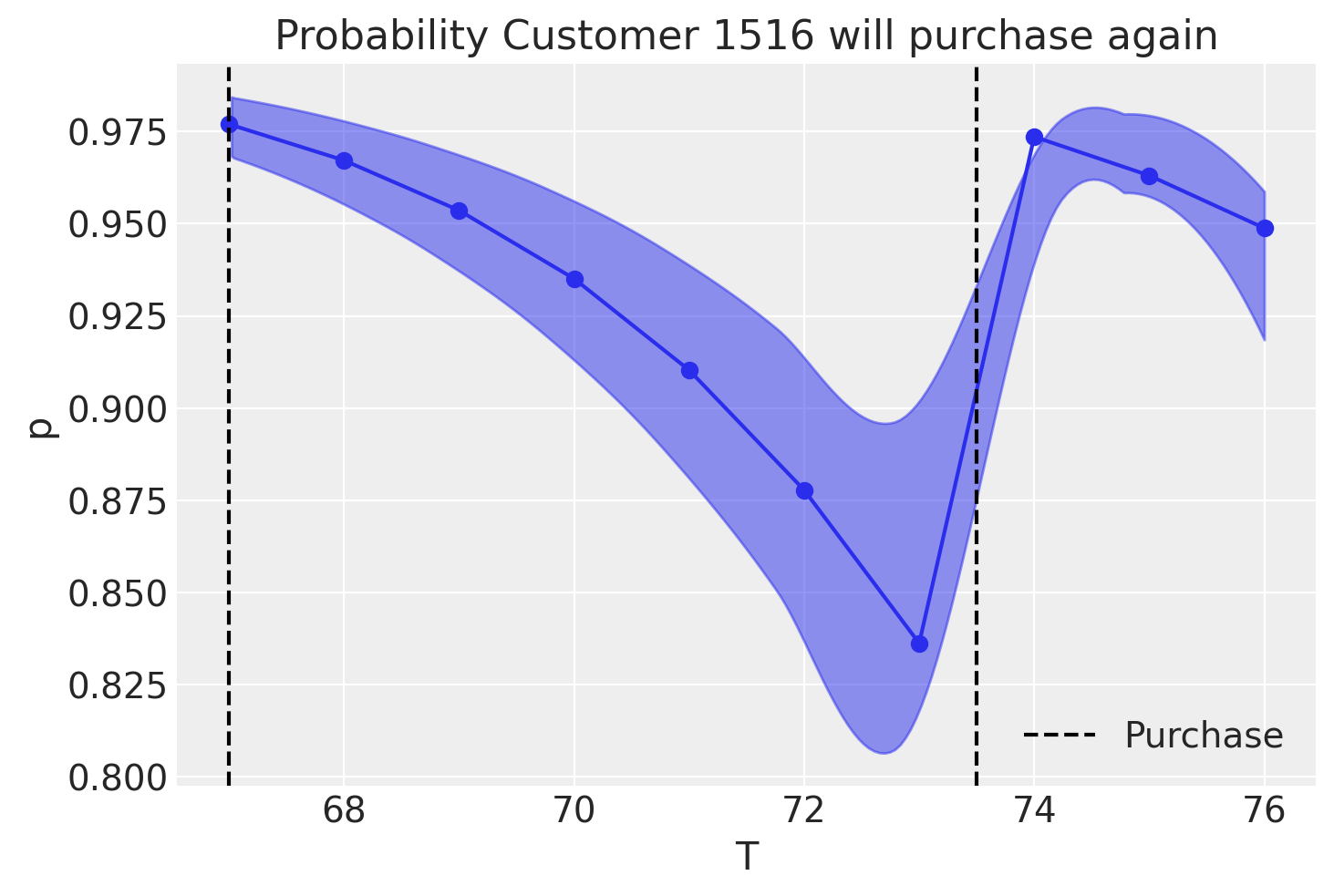
customer_1516_history.loc[7:,"frequency"] += 1
customer_1516_history.loc[7:,"recency"] = customer_1516_history.loc[7,"T"] - 0.5
customer_1516_history

	ID	frequency	recency	T
0	1515	27	67.0	67
1	1515	27	67.0	68
2	1515	27	67.0	69
3	1515	27	67.0	70
4	1515	27	67.0	71
5	1515	27	67.0	72
6	1515	27	67.0	73
7	1515	28	73.5	74
8	1515	28	73.5	75
9	1515	28	73.5	76

p_alive = bgm.expected_probability_alive(
    customer_id=customer_1516_history["ID"],
    frequency=customer_1516_history["frequency"],
    recency=customer_1516_history["recency"],
    T=customer_1516_history["T"],
)

az.plot_hdi(customer_1516_history["T"], p_alive, color="C0")
plt.plot(customer_1516_history["T"], p_alive.mean(("draw", "chain")), marker="o")
plt.axvline(customer_1516_history["recency"].iloc[0], c="black", ls="--", label="Purchase")
plt.axvline(customer_1516_history["recency"].iloc[-1], c="black", ls="--")

plt.title("Probability Customer 1516 will purchase again")
plt.xlabel("T")
plt.ylabel("p")
plt.legend();

From the plot above, say that customer 1516 makes a purchase at week 73.5, just over 6 weeks after they have made their last recorded purchase. We can see that the probability of the customer returning quickly goes back up!

Estimating Customer Lifetime Value Using the Gamma-Gamma Model

Until now we’ve focused mainly on transaction frequencies and probabilities, but to estimate economic value we can use the Gamma-Gamma model.

The Gamma-Gamma model assumes at least 1 repeat transaction has been observed per customer. As such we filter out those with zero repeat purchases.

nonzero_data = rfm_data.query("frequency>0")
nonzero_data

	customer_id	frequency	recency	T	monetary_value
0	1	3.0	49.0	78.0	23.723333
1	2	1.0	2.0	78.0	11.770000
5	6	14.0	76.0	78.0	76.503571
6	7	1.0	5.0	78.0	11.770000
7	8	1.0	61.0	78.0	26.760000
...	...	...	...	...	...
2351	2352	1.0	47.0	66.0	14.490000
2352	2353	2.0	53.0	66.0	19.775000
2353	2354	5.0	24.0	66.0	44.928000
2354	2355	1.0	44.0	66.0	24.600000
2355	2356	6.0	62.0	66.0	31.871667

1126 rows × 5 columns

If computing the monetary value from your own data, note that it is the mean of a given customer’s value, not the sum. monetary_value can be used to represent profit, or revenue, or any value as long as it is consistently calculated for each customer.

The Gamma-Gamma model relies upon the important assumption there is no relationship between the monetary value and the purchase frequency. In practice we need to check whether the Pearson correlation is less than 0.3:

nonzero_data[['monetary_value', 'frequency']].corr()

	monetary_value	frequency
monetary_value	1.000000	0.052819
frequency	0.052819	1.000000

Transaction frequencies and monetary values are uncorrelated; we can now fit our Gamma-Gamma model to predict average spend and expected lifetime values of our customers

The Gamma-Gamma model takes in a ‘data’ parameter, a pandas DataFrame with 3 columns representing Customer ID, average spend of repeat purchases, and number of repeat purchase for that customer. As with the BG/NBD model, these parameters are given HalfFlat priors which can be too diffuse for small datasets. For this example, we will use the default priors, but other priors can be specified just like with the BG/NBD example above.

dataset = pd.DataFrame({
    'customer_id': nonzero_data.index,
    'mean_transaction_value': nonzero_data["monetary_value"],
    'frequency': nonzero_data["frequency"],
})

gg = clv.GammaGammaModel(
    data = dataset
)
gg.build_model()
gg

Gamma-Gamma Model (Mean Transactions)
         p ~ HalfFlat()
         q ~ HalfFlat()
         v ~ HalfFlat()
likelihood ~ Potential(f(q, p, v))

By default, fit approximates full Bayesian posterior using MCMC sampling provided by pymc.sample. If the full posterior is not needed or MCMC sampling is too slow, users can obtain the single maximum a posteriori estimate via the fit_method kwarg.

gg.fit(fit_method="map");

100.00% [24/24 00:00<00:00 logp = -4,899.8, ||grad|| = 17.939]

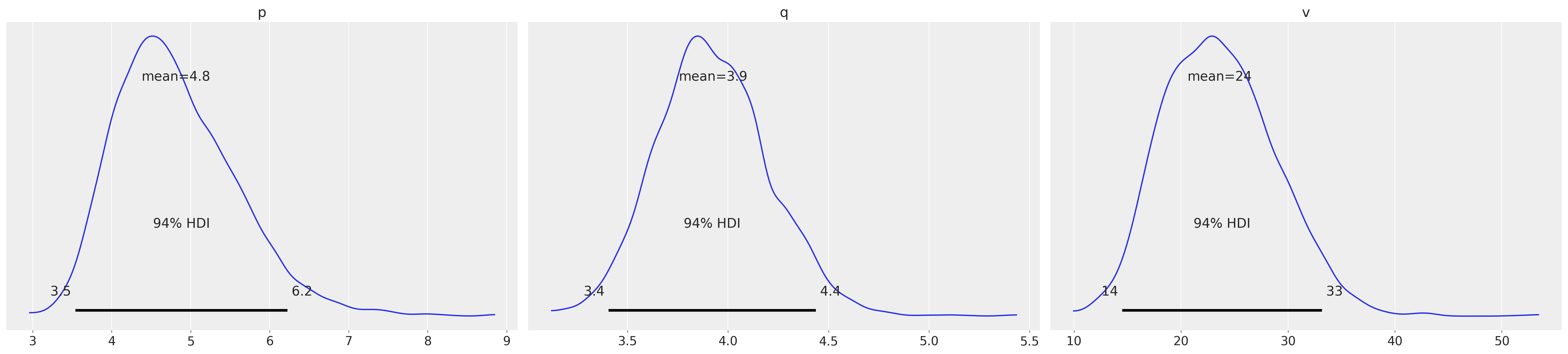
gg.fit_summary()

p     4.785
q     3.882
v    22.653
Name: value, dtype: float64

gg.fit();

Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [p, q, v]

100.00% [8000/8000 00:04<00:00 Sampling 4 chains, 0 divergences]

Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 5 seconds.

gg.fit_summary()

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
p	4.815	0.765	3.542	6.225	0.026	0.019	857.0	1022.0	1.0
q	3.926	0.280	3.407	4.437	0.010	0.007	772.0	1087.0	1.0
v	23.605	5.230	14.497	33.175	0.188	0.133	762.0	945.0	1.0

az.plot_posterior(gg.fit_result);

Predicting spend value of customers

Having fit our model, we can now use it to predict the conditional, expected average lifetime value of our customers, including those with zero repeat purchases.

expected_spend = gg.expected_customer_spend(
    customer_id=rfm_data.index,
    mean_transaction_value=rfm_data["monetary_value"],
    frequency=rfm_data["frequency"],
)

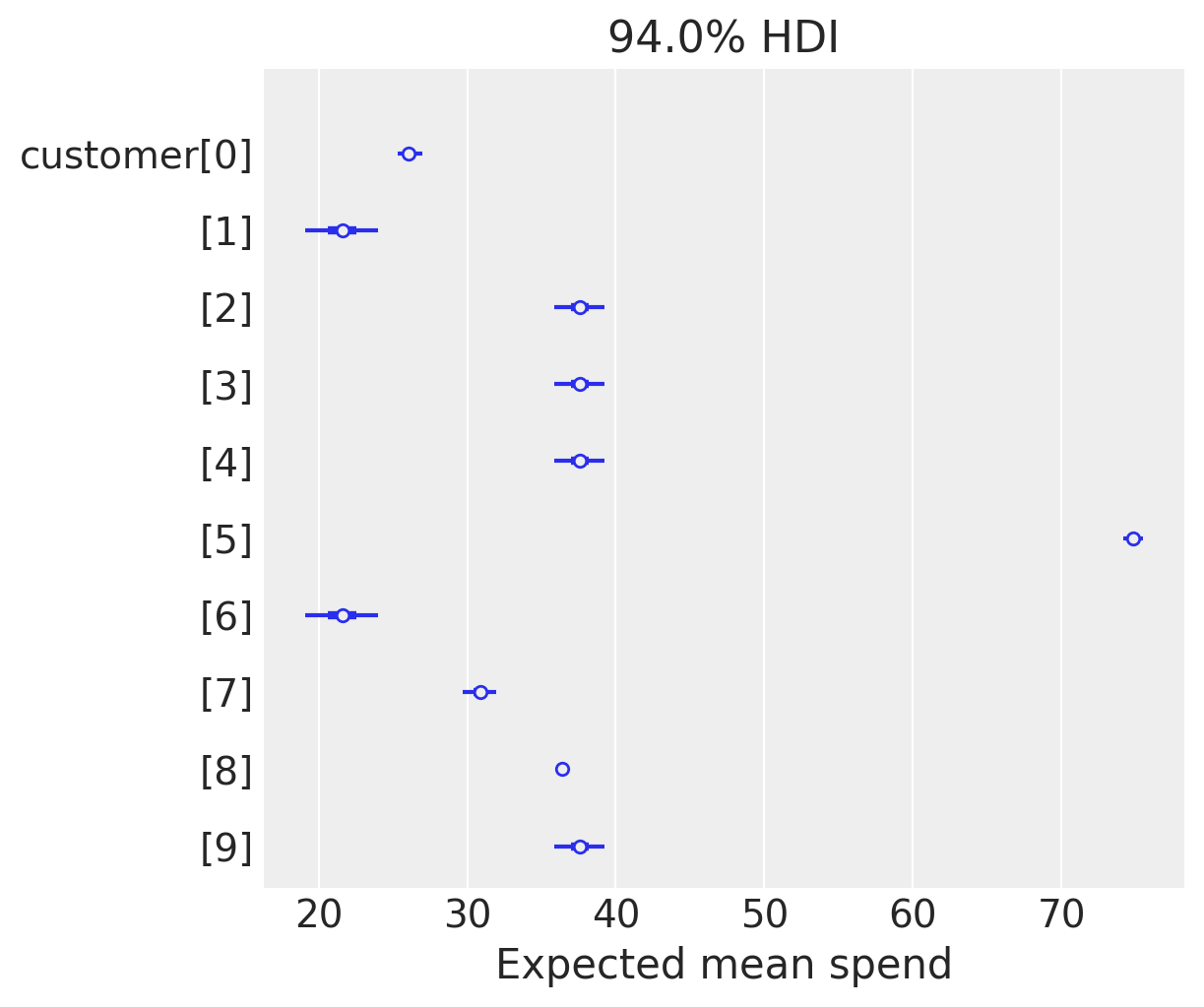
az.summary(expected_spend.isel(customer_id=range(10)), kind="stats")

	mean	sd	hdi_3%	hdi_97%
x[0]	26.106	0.442	25.342	26.950
x[1]	21.616	1.348	19.113	24.008
x[2]	37.615	0.901	35.848	39.215
x[3]	37.615	0.901	35.848	39.215
x[4]	37.615	0.901	35.848	39.215
x[5]	74.836	0.366	74.151	75.475
x[6]	21.616	1.348	19.113	24.008
x[7]	30.890	0.617	29.705	31.974
x[8]	36.430	0.155	36.148	36.732
x[9]	37.615	0.901	35.848	39.215

labeller = MapLabeller(var_name_map={"x": "customer"})
az.plot_forest(expected_spend.isel(customer_id=(range(10))), combined=True, labeller=labeller)
plt.xlabel("Expected mean spend");

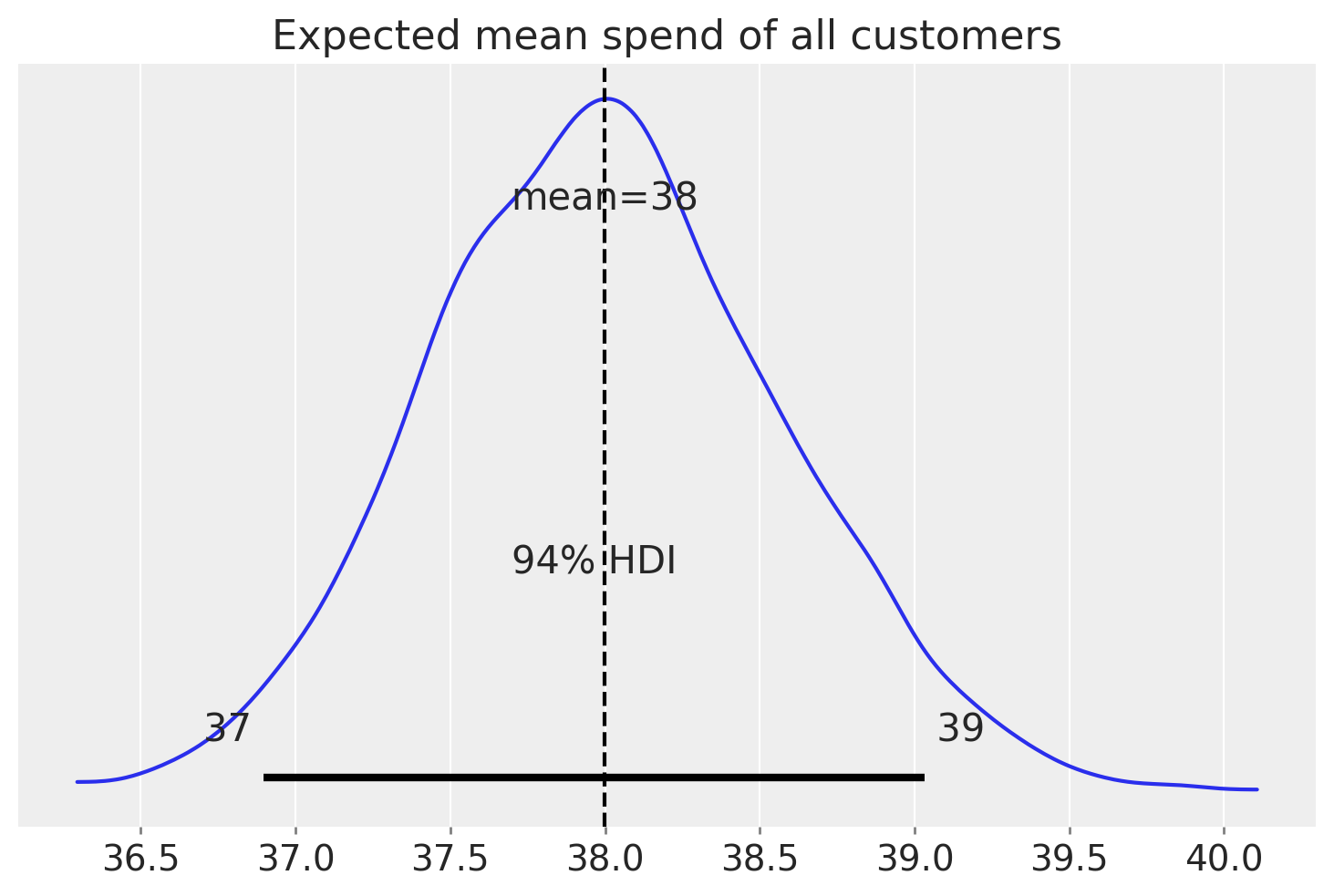
We can also look at the average expected mean spend across all customers

az.summary(expected_spend.mean("customer_id"), kind="stats")

	mean	sd	hdi_3%	hdi_97%
x	38.0	0.568	36.898	39.033

az.plot_posterior(expected_spend.mean("customer_id"))
plt.axvline(expected_spend.mean(), color="k", ls="--")
plt.title("Expected mean spend of all customers");

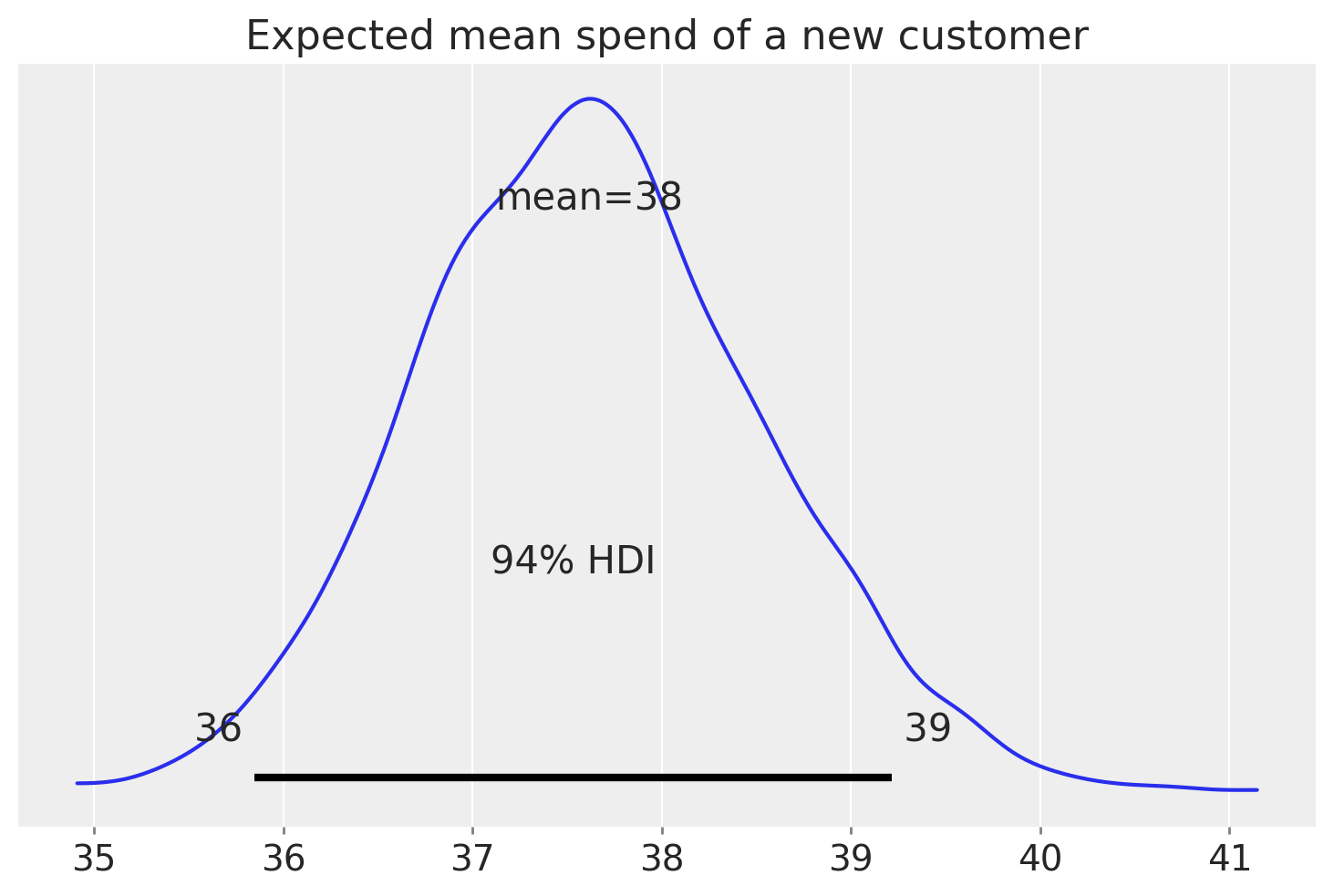
Predicting spend value of a new customer

az.plot_posterior(
    gg.expected_new_customer_spend()
)
plt.title("Expected mean spend of a new customer");

Estimating CLV

Finally, we can combine the GG with the BG/NBD model to obtain an estimate of the customer lifetime value. This relies on the Discounted cash flow model, adjusting for cost of capital:

clv_estimate = gg.expected_customer_lifetime_value(
    transaction_model=bgm,
    customer_id=rfm_data.index,
    mean_transaction_value=rfm_data["monetary_value"],
    frequency=rfm_data["frequency"],
    recency=rfm_data["recency"],
    T=rfm_data["T"],
    time=12, # months
    discount_rate=0.01, # monthly discount rate ~ 12.7% annually
    freq="W", # Our original data is in weeks
)

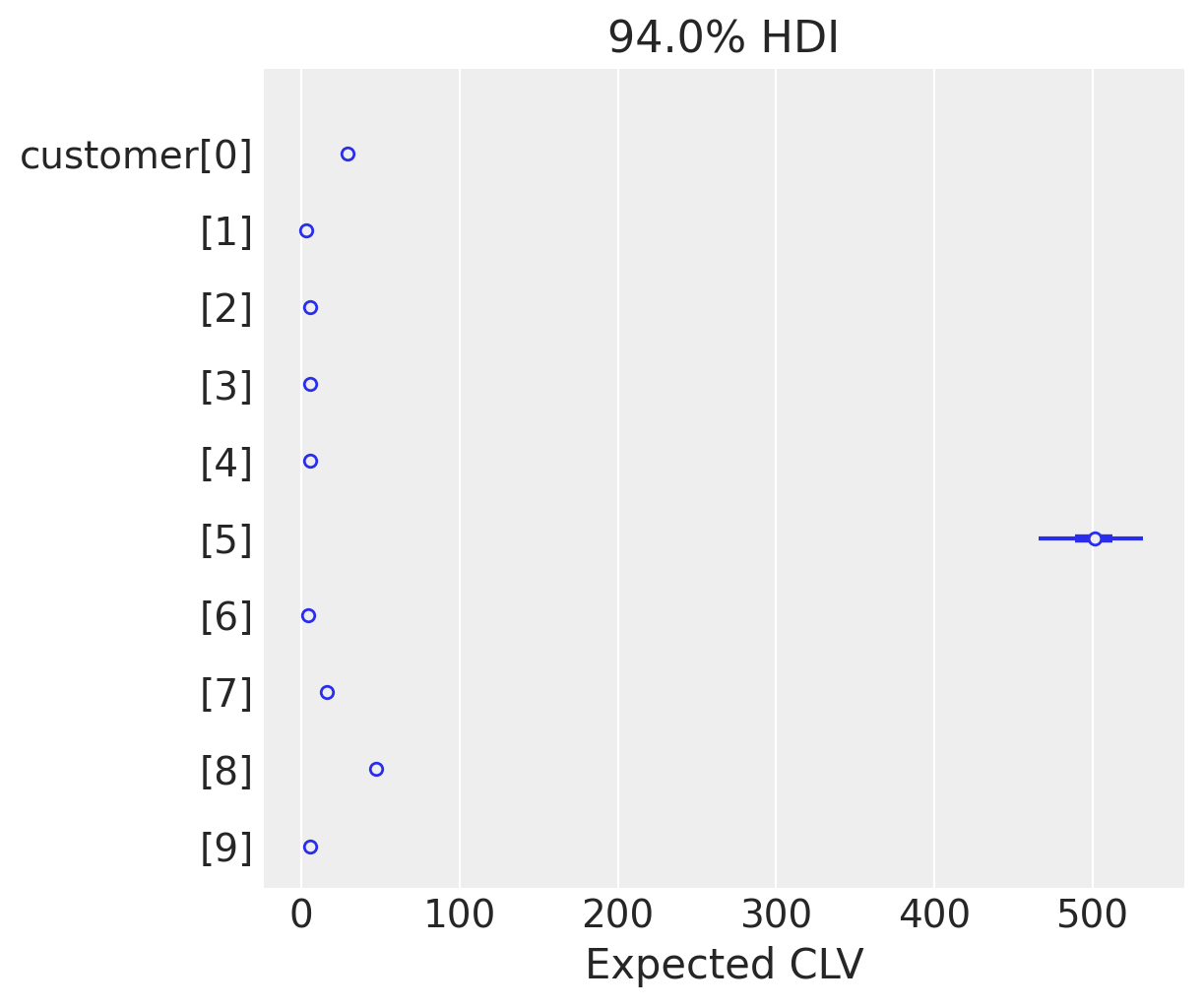
az.summary(clv_estimate.isel(customer_id=range(10)), kind="stats")

	mean	sd	hdi_3%	hdi_97%
x[0]	29.210	1.147	27.022	31.329
x[1]	3.107	0.365	2.419	3.767
x[2]	5.616	0.259	5.129	6.097
x[3]	5.616	0.259	5.129	6.097
x[4]	5.616	0.259	5.129	6.097
x[5]	500.478	17.735	466.030	531.913
x[6]	4.086	0.435	3.244	4.867
x[7]	16.218	0.542	15.173	17.193
x[8]	46.846	1.349	44.380	49.410
x[9]	5.616	0.259	5.129	6.097

az.plot_forest(clv_estimate.isel(customer_id=range(10)), combined=True, labeller=labeller)
plt.xlabel("Expected CLV");

According to our models, customer[5] has a much higher expected CLV. There is also a large variability in this estimate that arises solely from uncertainty in the parameters of the BG/NBD and GG models.

In general, these models tend to induce a strong correlation between expected CLV and uncertainty. This modelling of uncertainty can be very useful when making marketing decisions.